Memorator PM
Haide, Moga, recita egloga, ca la Stroia bate nevoia
Contents
- Suspectez ca trebuie sa folosesc functia salcfxyz dar am uitat cum o folosesc, ce fac???
- Cum fac o functie?
- Cum fac graficul unei functii?
- + Cum plotuiesc mai multe lucruri simultan, unul peste altul?
- + Cum plotuiesc mai multe lucruri simultan, in figuri diferite?
- Cum aflu o solutie a unei ecuatii diferentiale?
- Cum aproximez o serie de date masurate folosind un polinom de gradul 1 sau 2?
- Cum ma folosesc de aproximare?
- Cum verific / plotuiesc erorile unei astfel de aproximari?
- Functii utile
- Cum aproximez o potriveala liniara intre mai multe variabile?
- Cum modelez un sistem mecanic ca un circuit electric?
- Integrare cu trapz
- Cum rezolv un sistem dubios de ecuatii? (posibil neliniare)
- Cum modelam sisteme cu tevi?
Suspectez ca trebuie sa folosesc functia salcfxyz dar am uitat cum o folosesc, ce fac???
Daca iti suna cunoscut exercitiul la care lucrezi si crezi ca o sa te ajute o anumita functie, say fplot, dar ai uitat cum sa o folosesti, vezi daca cumva te ajuta documentatia MATLAB. Doar scrii doc fplot in consola de jos (sau doc functsia_tha pe caz general) si o sa iti apara documentatie cu descriere, parametri, exemple de cod cu desene. Nu poti invata usor de pe documentatia aia, dar poate ajuta sa iti aminteasca cate ceva!
Cum fac o functie?
Cu function lmao. Jokes, aside, trebuie sa ne gandim:
1. Cum se numeste functia? Facem un fisier cu numele ala.
2. Ce parametri primeste? Daca e o functie in timp, primeste un t. Daca e o functie data lui ode, primeste un timp t si o stare x. Daca e o functie data lui fsolve, primeste un vector x. Etc etc etc.
3. Ce returneaza?
function functie_care_nu_returneaza_nimic_si_nu_primeste_nimic() disp("Salut! Eu nu fac nimic..."); end function x = functie_care_returnaza_dar_nu_primeste_nimic() x = sin(123); end function functie_care_primeste_dar_nu_returneaza(a, b) fprintf("a=%d si b=%d\n", a, b); end function y = functie_care_si_primeste_si_returneaza(x) if x > 1 && x < 4 y = sin(x*3)+1; else y = -3; end end
Cum fac graficul unei functii?
Hai sa spunem, functia asta:
\[ y = \begin{cases} (t^3 - 1) \cdot (t + 1)\text{, pentru }t \in (10, 44) \\ t \cdot (4t + 3t - 12)\text{, pentru }t \not\in (10, 44) \end{cases} \]
Pe intervalul \([0, 100]\). Implementata in MATLAB ar fi:
function y = par(t) if t>10 && t<44 y=(t^3-1)*(t+1); else y=t*(4*t +3*t-12); end end
(numele de par a fost ales la intamplare)
Daca vrem sa il lasam pe autopilot si doar sa ii zicem de unde pana unde sa ne faca graficul, folosim fplot si ii dam numele functiei cu @ (@par) sau intre apostroafe ('par', nerecomandat) si un interval pt x-uri:
fplot(@par, [0, 100]); % sau fplot('par', [0, 100]); % dar la asta se plange ca e deprecated, scrie si % in warnings.
Warning: Function behaves unexpectedly on array inputs. To improve performance, properly vectorize your function to return an output with the same size and shape as the input arguments. Warning: fplot will not accept character vector or string inputs in a future release. Use fplot(@par) instead. Warning: Function behaves unexpectedly on array inputs. To improve performance, properly vectorize your function to return an output with the same size and shape as the input arguments.
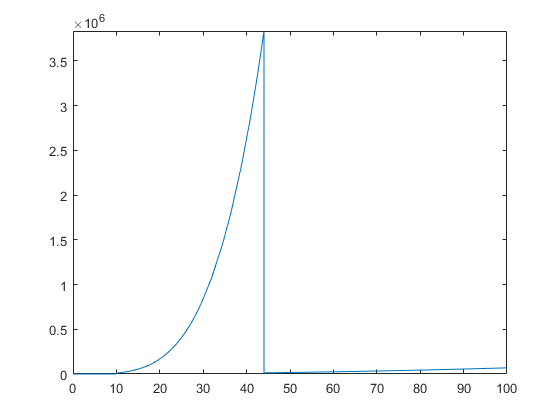
Varianta 2 e sa folosim plot daca vrem sa ii dam niste perechi (abscisa, ordonata) anume. Ar fi cazul cand ne da dume d'alea cu "8000 samples per second" care inseamna ca vrea sa avem 8000 de puncte per unitate pe axa X, caz in care vrem sa avem distanta dintre puncte de 1/8000:
sample_rate = 8000; distanta_intre_puncte = 1/sample_rate; turi = 0:distanta_intre_puncte:100; yuri = []; for i=1:length(turi) yuri(i)=par(turi(i)); end plot(turi,yuri);
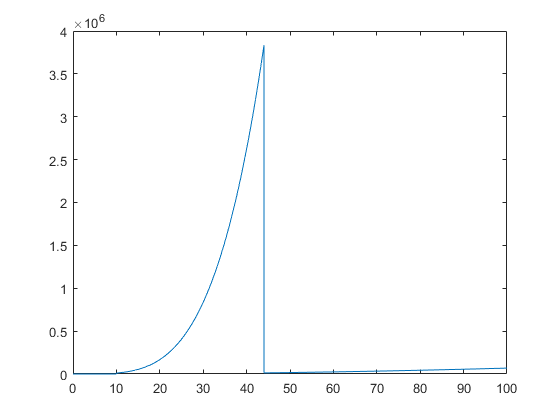
+ Cum plotuiesc mai multe lucruri simultan, unul peste altul?
Zici hold on inainte sa incepi sa apelezi functii care deseneaza (plot, fplot, errorbar, etc). Poti da si clf ca sa stergi ce era inainte pe figura, dar sa vina inainte de hold on.
+ Cum plotuiesc mai multe lucruri simultan, in figuri diferite?
Poti deschide o fereastra noua cu un plot nou folosind figure. Grija, insa, ca odata ce ai deschis un plot nou nu mai e usor sa te intorci la figurile vechi sa mai adaugi/schimbi ceva.
Cum aflu o solutie a unei ecuatii diferentiale?
Vine Mogix la gagica-ta si ii zice ca vrea sa vada cum evolueaza un sistem modelat de ecuatia asta diferentiala:
\[ \frac{dx}{dt} = 4 \cdot m_{oga}(t) - 3x \]
unde
\[ m_{oga}(t) = \begin{cases} sin(4\pi t),\quad t\in(0, 2) \\ 0.5,\quad t\not\in(0, 2) \end{cases} \]
Care incepe cu \(x(0) = 1\), pe intervalul de timp \(t \in [0; 10]\).
Ce faci??????
Fear no more, automatistx, ca avem niste cod greu de urmarit!
Prima data, implementam undeva parametrica lui Moga:
function moga = plm(t) if t > 0 && t < 2 moga = sin(4 * pi * t); else moga = 0.5; end end
Dupa, si aici e partea esentiala, trebuie sa facem o functie care primeste un timp t si lucrul pe care il studiem in timp x si returneaza derivata lui la timpul t:
function dx = derivata_lu_moga(t, x) dx = 4 * plm(t) - 3 * x; end
De exemplu, daca apelam functia asta cu conditiile initiale t=0, x=1, functia ne da derivata lui x in acel moment:
derivata_lu_moga(0, 1)
ans =
-1
Acum ca avem aceasta functie care descrie sistemul, ne folosim de ode23 sau ode45 sa ne afle automat cum evolueaza el in timp. Ii dam, ca la fplot, numele functiei, dupa intervalul de timp, si in plus mai punem si conditiile initiale:
[t, x] = ode45(@derivata_lu_moga, [0, 10], 1);
Functia asta ne da un vector cu niste puncte in timp si un vector cu valorile lui x in acele momente. Nu e usor de prezis cand vor fi aceste puncte, dar vor fi destul de multe cat sa deseneze ok functia, usually:
plot(t, x);
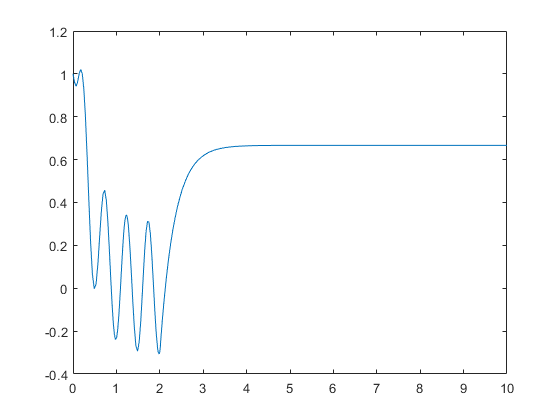
Cum aproximez o serie de date masurate folosind un polinom de gradul 1 sau 2?
In multe exercitii ni se dau serii de date cum ar fi aceasta curba caracteristica a unei pompe:
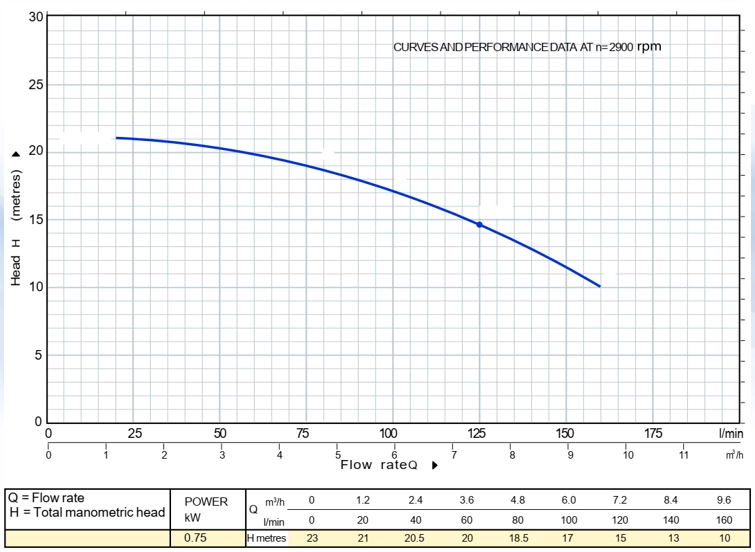
Cu tabelul de date de jos, care transcris in cod este:
date_x = [ 0 20 40 60 80 100 120 140 160]'; date_y = [23 21 20.5 20 18.5 17 15 13 10 ]';
Si noi trebuie sa facem o aproximare liniara sau de gradul 2 care are, in linii mari, acelasi comportament cu punctele date. Pentru asta folosim fit ca sa facem aproximarea si coeffvalues ca sa scoatem din ea coeficientii polinomului:
% Aproximare de gradul 1 fit1 = fit(date_x, date_y, 'poly1'); coeficienti1 = coeffvalues(fit1); a = coeficienti1(1); b = coeficienti1(2); aprox_y_1 = date_x * a + b; % Aproximare de gradul 2 fit2 = fit(date_x, date_y, 'poly2'); coeficienti2 = coeffvalues(fit2); a = coeficienti2(1); b = coeficienti2(2); c = coeficienti2(3); aprox_y_2 = date_x .^ 2 * a + date_x * b + c; % Grija sa fie .^ nu ^ % Desenam clf; hold on; plot(date_x, date_y, '+b'); plot(date_x, aprox_y_1, 'r'); plot(date_x, aprox_y_2, 'g'); legend(["date masurate", "aproximare gradul 1", "aproximare gradul 2"]); hold off;
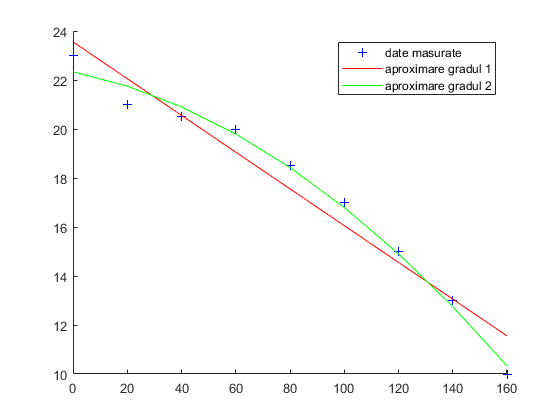
Cum ma folosesc de aproximare?
Odata ce avem coeficientii unei aproximari, putem sa punem intrebari de genul "care ar fi y-ul corespunzator lui x=1.2345? x care nu apare in datele initiale", ca doar asta le e rostul - sa scoatem o formula generala din o lista finita de puncte.
De exemplu, pentru ca mie mi-au ramas in variabilele a, b, c coeficientii aproximarii de gradul 2, pot calcula valorile ei in puncte arbitrare asa:
x = 1.2345; y = x^2 * a + x * b + c;
Si ne da ca y =...
disp(y)
22.3049
Cum verific / plotuiesc erorile unei astfel de aproximari?
Odata ce am facut o aproximare cu fit, putem sa si verificam cat de bine se potriveste punctelor date. Metrica folosita cel mai des si pe care ne-o cere Mogix la teste este "suma patratelor diferentelor". Adica, daca avem câteva puncte măsurate \((x_1,y_1),\dots,(x_n,y_n)\) si aproximarile in x-urile alea \((x_1,y_{aprox,1}),\dots(x_n,y_{aprox,n})\). Vom calcula diferentele intre y-urile masurate si cele prezise de aproximare:
\[ \Delta_1 = y_1 - y_{aprox,1};\ \dots;\ \Delta_n = y_n - y_{aprox,n} \]
Le vom ridica la patrat pe fiecare si le vom face suma:
\[ \text{err} = \sum_{i=1}^n (y_i - y_{aprox,i})^2 \]
Daca rezultatul ala e mic (cat de mic depinde de aplicatie, dar la test nu e pt noi sa judecam asta) atunci aproximarea e buna. Daca e mare, aproximarea e rea. 0 e perfect.
erori_gradul1 = aprox_y_1 - date_y; erori_gradul2 = aprox_y_2 - date_y; err1 = sum(erori_gradul1 .^ 2) err2 = sum(erori_gradul2 .^ 2)
err1 =
6.7222
err2 =
1.4405
Putem sa mai aratam grafic erorile folosind errorbar. Are sintaxa similara lui plot, in sensul ca primeste un vector de x-uri si unul de y-uri, dar mai primeste inca un vector care ne zice eroarea in fiecare punct:
% in loc de: % plot(date_x, aprox_y_1); % zicem: errorbar(date_x, aprox_y_1, erori_gradul1);
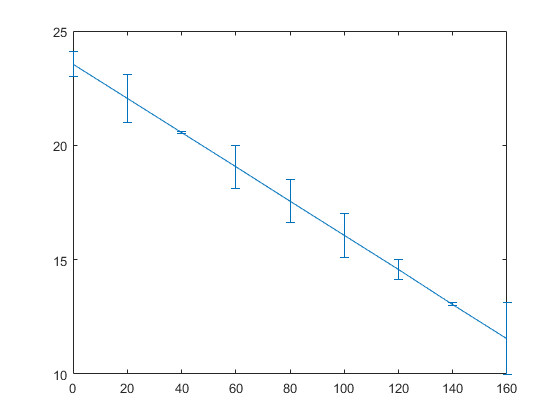
errorbar(date_x, aprox_y_2, erori_gradul2);
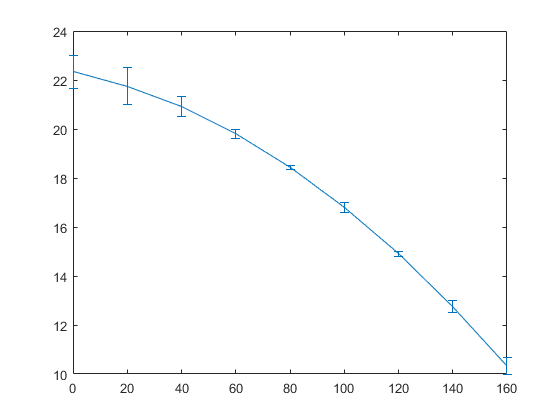
Functii utile
min si max ne dau elementul minim si maxim dintr-un vector. mean ne face media aritmetica a valorilor dintr-un vector. std ne calculeaza deviatia standard a valorilor dintr-un vector. sum ne face suma elementelor unui vector. length ne zice lungimea unui vector.
Cum aproximez o potriveala liniara intre mai multe variabile?
Uneori (lab6) dam de niste date in mai multe variabile despre care stim ca sunt roughly intr-o relatie liniara:
\[ P \approx a \cdot X + b \cdot Y \]
Lucrul asta accepta si sa avem un termen liber \(c\):
\[ P \approx a \cdot X + b \cdot Y + c \]
Dar pe care trebuie sa il asociem unui vector cu 1:
\[ P \approx a \cdot X + b \cdot Y + c \cdot \begin{pmatrix}1 \\ \vdots \\ 1\end{pmatrix} \]
Odata ce aducem sistemul nostru de aproximari la forma asta
\[ \begin{cases} P_1 \approx a \cdot X_1 + b \cdot Y_1 + c \cdot 1 \\ P_2 \approx a \cdot X_2 + b \cdot Y_2 + c \cdot 1 \\ \dots \\ P_n \approx a \cdot X_n + b \cdot Y_n + c \cdot 1 \end{cases} \]
care e echivalenta cu
\[ \begin{pmatrix}P_1 \\ P_2 \\ \vdots \\ P_n\end{pmatrix} \approx a \cdot \begin{pmatrix}X_1 \\ X_2 \\ \vdots \\ X_n\end{pmatrix} + b \cdot \begin{pmatrix}Y_1 \\ Y_2 \\ \vdots \\ Y_n\end{pmatrix} + c \cdot \begin{pmatrix}1 \\ 1 \\ \vdots \\ 1\end{pmatrix} \]
Folosim functia regress. Ea primeste ca prim parametru ce e in stanga semnului \(\approx\), ca vector coloana. Al doilea parametru e un vector de vectori coloana (i.e. o matrice) care corespund vectorilor din dreapta. Returneaza un vector cu coeficientii nostri \(a,b,c\) in ordine.
Pe exemplu concret, in lab6 avem urmatorul tabel:
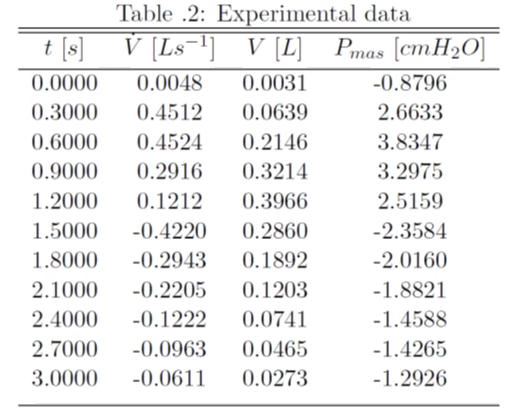
Care descrie o serie de masuratori in 3 variabile: \(P\), \(V\) si \(V'\) despre care stim ca au o relatie cam liniara:
\[ P \approx E_L \cdot V + R_t \cdot V' + P_0 \]
Dar unde \(E_L\), \(R_t\) si \(P_0\) sunt niste coeficienti pe care ar trebui noi sa ii potrivim cat sa fie aproximarea cat mai buna.
Avand vectori cu datele \([P_1,\dots,P_n]^t\), \([V_1,\dots, V_n]^t\), \([V'_1,\dots,V'_n]^t\):
t = 0:0.3:3;
Vprim = [
0.048; 0.4512; 0.4524; 0.2916; 0.1212; -0.4220; -0.2943; -0.2205; ...
-0.1222; -0.0965; -0.0611
];
V = [
0.0031; 0.0639; 0.2146; 0.3214; 0.3966; 0.2860; 0.1892; 0.1203; ...
0.0741; 0.0465; 0.0273
];
P = [
-0.8796; 2.6633; 3.8347; 3.2975; 2.5159; -2.3584; -2.0160; -1.8821; ...
-1.4588; -1.4265; -1.2926
];
Putem sa ii dam lui regress in ordinea buna sa incerce sa ne gaseasca niste coeficienti dragutsi:
coeficienti = regress(P, [V, Vprim, ones(length(P), 1)]); el = coeficienti(1); rt = coeficienti(2); p0 = coeficienti(3);
Pe care ii putem folosi sa vedem cum aproximeaza el P-urile:
P_approx = el * V + rt * Vprim + p0;
Si desena ca sa le comparam, eventual chiar cu error bars:
erori = P - P_approx; clf; hold on; plot(t, P, 'b+'); errorbar(t, P_approx, erori);
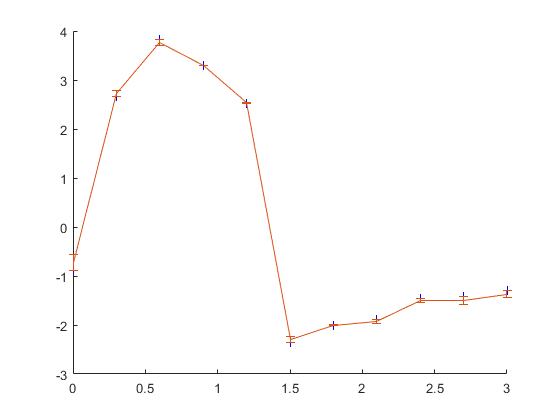
Error bar-urile is asa de mici ca abia se vad, deci avem o aproximare destul de buna. Daca vrem, am putea face un exercitiu de statistica sa vedem suma patratelor erorilor ca sa si cuantificam cat de buna e aproximarea:
sum(erori .^ 2)
ans =
0.0542
Numarul asta nu are sens by itself, dar poate fi comparat cu unul al altei aproximari pe aceleasi date. Care aproximare are numarul asta mai mic e mai buna pe punctele din setul de date.
Cum modelez un sistem mecanic ca un circuit electric?
Daca avem un sistem mecanic format doar din: puncte materiale (cu masa), amortizoare (cu coeficient de frecare), arcuri (cu coeficient elastic), si am vrea sa il simulam in timp, putem sa ne folosim de Analogia electromecanica, care ne spune cum sa transformam acest sistem intr-un circuit electric care se va comporta numeric identic. Asta inseamna ca marimile fizice din sistemul mecanic pot fi traduse numeric in marimi fizice din circuit si totul se va comporta la fel.
Ne folosim de urmatorul tabel:
| Electric | Mechanic | Conversion | ||
| Parameter | Relation: \(i(t) \to u(t)\) | Parameter | Relation: \(f(t) \to v(t)\) | |
| \( u(t) \) | \( v(t) \) | |||
| \( i(t) \) | \( f(t) \) | |||
| \(R\) | \( u(t) = Ri(t) \) | \(B\) | \( v(t) = \frac{1}{B} f(t) \) | \( B = 1/R \) |
| \(C\) | \( \frac{du(t)}{dt} = \frac{i(t)}{C} \) | \(M\) | \(\frac{dv(t)}{dt} = \frac{f(t)}{M}\) | \( M = C \) |
| \(L\) | \( u(t) = L \frac{di(t)}{dt} \) | \(K\) | \( v(t) = \frac{df(t)}{dt} / K \) | \( L = 1/K \) |
care ne zice ca daca traducem viteza mecanica \(v\) in tensiune electrica \(u\), forta mecanica \(f\) in intensitatea curentului electric \(i\), coeficientul de frecare vascoasa (dar inversat) \(1/B\) in rezistenta electrica \(R\), masa mecanica \(M\) in capacitate electrica \(C\) si coeficientul elastic (dar inversat) \(1/L\) in inductanta electrica \(L\), numerele se vor comporta la fel in timp.
In lab 7, avem urmatorul sistem care rezuma roata unei masini pe un teren accidentat:
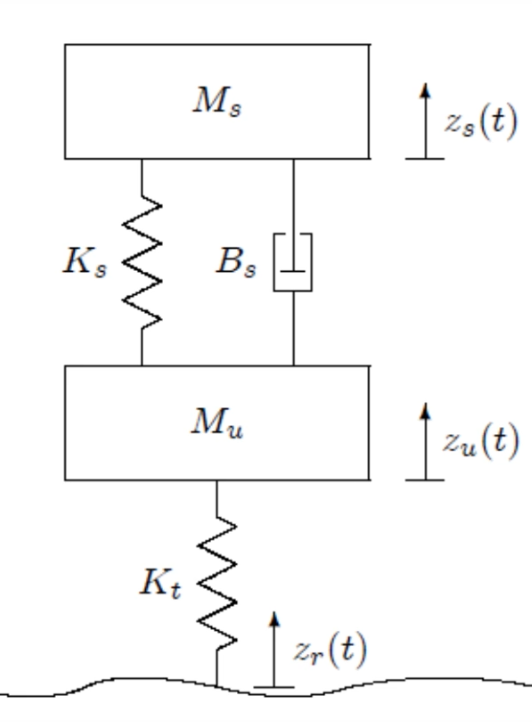
Vom transforma masele in condensatoare cu un capat la ground, iar arcurile si amortizorul in inductori, respectiv rezistori, care se leaga la celelalte capete ale condensatoarelor:
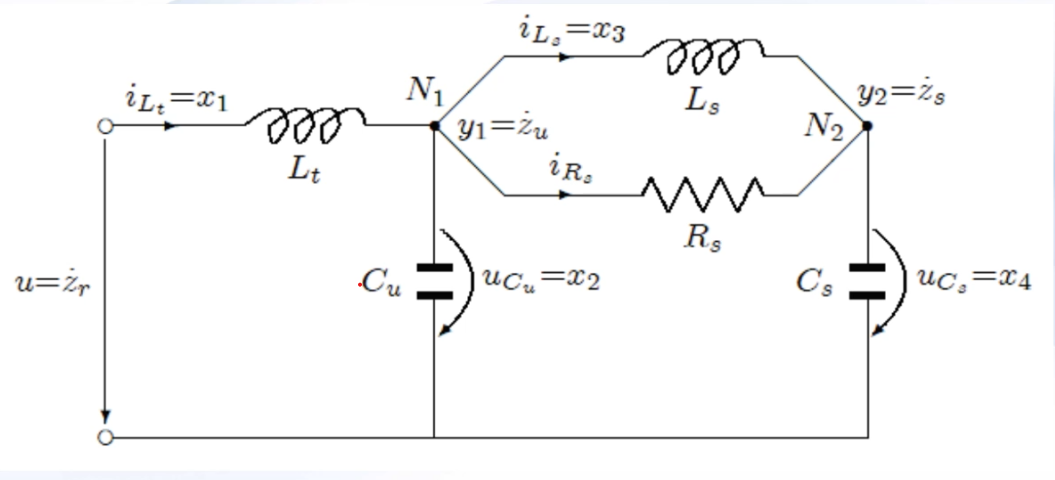
As per usual, daca vrem sa simulam asta in timp, vom analiza intensitatea prin inductori (\(i_{L_t}, i_{L_s}\)) si tensiunea prin condensatoare (\(u_{C_u}, u_{C_s}\)).
Cu niste Kirchoff si Ohm, dam de urmatoarele formule (nu le-am facut de mana, le-am luat din lab. La test, daca da ceva de genul, they better give us these)
\[ \begin{aligned} \frac{di_{L_t}}{dt} &= - \frac{1}{L_t} u_{C_u} \\ \frac{du_{C_u}}{dt} &= \frac{1}{C_u} i_{L_t} - \frac{1}{R_sC_u} u_{C_u} - \frac{1}{C_u} i_{L_s} + \frac{1}{R_sC_u} u_{C_s} \\ \frac{di_{L_t}}{dt} &= \frac{1}{L_s} u_{C_u} - \frac{1}{L_s} u_{C_s} \\ \frac{du_{C_s}}{dt} &= \frac{1}{R_sC_s} u_{C_u} + \frac{1}{C_s} i_{L_s} - \frac{1}{R_sC_s} u_{C_s} \end{aligned} \]
Care, daca ne folosim iar de analogia electromecanica, devine:
\[ \begin{aligned} \frac{df_{K_t}}{dt} &= - K_t v_{M_u} \\ \frac{dv_{M_u}}{dt} &= \frac{1}{M_u} f_{K_t} - \frac{B_s}{M_u} v_{M_u} - \frac{1}{M_u} f_{K_s} + \frac{B_s}{M_u} v_{C_s} \\ \frac{df_{K_t}}{dt} &= K_s v_{M_u} - K_s v_{C_s} \\ \frac{dv_{M_s}}{dt} &= \frac{B_s}{M_s} v_{M_u} + \frac{1}{M_s} f_{K_s} - \frac{B_s}{M_s} v_{C_s} \end{aligned} \]
De eleganta si tupeu, mai transformam asta intr-o matrice:
\[ \begin{pmatrix} \frac{df_{K_t}}{dt} \\ \frac{dv_{M_u}}{dt} \\ \frac{df_{K_t}}{dt} \\ \frac{dv_{M_s}}{dt} \end{pmatrix} = \begin{pmatrix} 0 & -K_t & 0 & 0 \\ 1/M_u & -B_s/M_u & -1/M_u & B_s / M_u \\ 0 & K_s & 0 & -K_s \\ 0 & B_s/M_s & 1/M_s & -B_s/M_s \end{pmatrix} \cdot \begin{pmatrix} f_{K_t} \\ v_{M_u} \\ f_{K_t} \\ v_{M_s} \end{pmatrix} + \begin{pmatrix} K_t \\ 0 \\ 0 \\ 0 \end{pmatrix} z_r \]
Pe care o putem simula cu ode!
function derivs = lab7ode(t, state) Ms = 300; Ks = 2800; Bs = 2000; Mu = 30; Kt = 21000; matrice1 = [... 0, -Kt, 0, 0 1/Mu, -Bs/Mu, -1/Mu, Bs/Mu 0, Ks, 0, -Ks 0, Bs/Ms, 1/Ms, -Bs/Ms]; matrice2 = [Kt; 0; 0; 0]; derivs = matrice1 * state + matrice2 * zr(t); end function road_height = zr(t) road_height = 0.1 * sin(20 * t) + 0.03 * sign(sin(5 * t)) + 0.02 * sign(sin(2 * t)); end
[t, states] = ode23(@lab7ode, [0, 10], [0; 0; 0; 0]);
Din states putem scoate coloanele care corespundeau vitezei masinii si a rotii:
v_roata = states(:, 2); v_masina = states(:, 4); clf; hold on; plot(t, v_masina); plot(t, v_roata); legend(["V masina", "V roata"]);
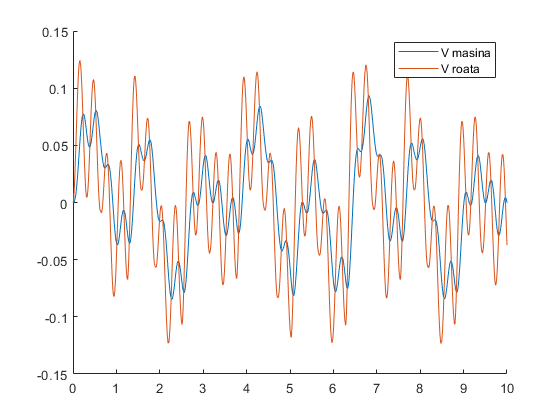
Si, eventual, sa deducem pozitiile din viteze, utilizand trapz.
Integrare cu trapz
Hai ca da
Cum rezolv un sistem dubios de ecuatii? (posibil neliniare)
fsolve baybee
Cum modelam sisteme cu tevi?
Dai un zorro