Lab 7, Ioan Dragomir

Process Modeling, prof. Daniel Moga, Technical University of Cluj-Napoca

Electromechanical analogy. Modeling a dampened mechnical system (car suspension) using an electric circuit.

Electric		Mechanic		Obs.
Parameter	Relation: \(i(t) \to u(t)\)	Parameter	Relation: \(f(t) \to v(t)\)
\( u(t) \)		\( v(t) \)
\( i(t) \)		\( f(t) \)
\(R\)	\( u(t) = Ri(t) \)	\(B\)	\( v(t) = \frac{1}{B} f(t) \)	\( B = 1/R \)
\(C\)	\( \frac{du(t)}{dt} = \frac{i(t)}{C} \)	\(M\)	\(\frac{dv(t)}{dt} = \frac{f(t)}{M}\)	\( M = C \)
\(L\)	\( u(t) = L \frac{di(t)}{dt} \)	\(K\)	\( v(t) = \frac{df(t)}{dt} / K \)	\( L = 1/K \)

\[ x(t) = \begin{pmatrix} i_{L_t}(t) \\ u_{C_u}(t) \\ i_{L_s}(t) \\ u_{C_s}(t) \end{pmatrix} \]

\[ \dot x(t) = \begin{pmatrix} \frac{di_{L_t}(t)}{dt} \\ \frac{du_{C_u}(t)}{dt} \\ \frac{di_{L_s}(t)}{dt} \\ \frac{du_{C_s}(t)}{dt} \end{pmatrix} = \begin{pmatrix} 0 & -\frac{1}{L_t} & 0 & 0 \\ \frac{1}{C_u} & -\frac{1}{R_sC_u} & -\frac{1}{C_u} & \frac{1}{R_sC_u} \\ 0 & \frac{1}{L_s} & 0 & -\frac{1}{L_s} \\ 0 & \frac{1}{R_sC_s} & \frac{1}{C_s} & -\frac{1}{R_sC_s} \end{pmatrix} \begin{pmatrix} i_{L_t}(t) \\ u_{C_u}(t) \\ i_{L_s}(t) \\ u_{C_s}(t) \end{pmatrix} + \begin{pmatrix} \frac{1}{L_t} \\ 0 \\ 0 \\ 0 \end{pmatrix} u\]

and, by the electromechanical analogy:

\[ \dot x(t) = \begin{pmatrix} 0 & -K_t & 0 & 0 \\ \frac{1}{M_u} & -\frac{B_s}{M_u} & -\frac{1}{M_u} & \frac{B_s}{M_u} \\ 0 & K_s & 0 & -K_s \\ 0 & \frac{B_s}{M_s} & \frac{1}{M_s} & -\frac{B_s}{M_s} \end{pmatrix} x(t) + \begin{pmatrix} K_t \\ 0 \\ 0 \\ 0 \end{pmatrix} z_r(t) \]

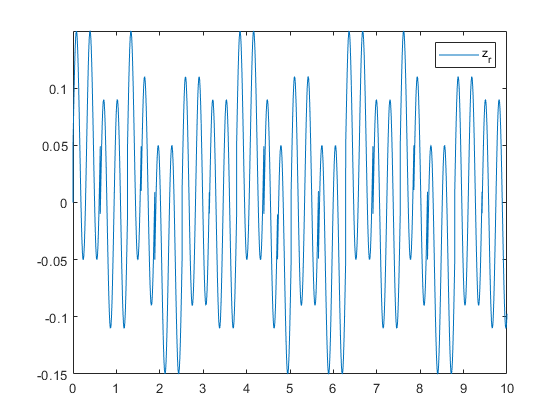
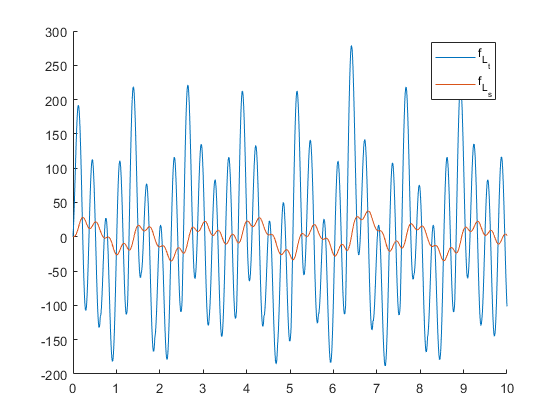
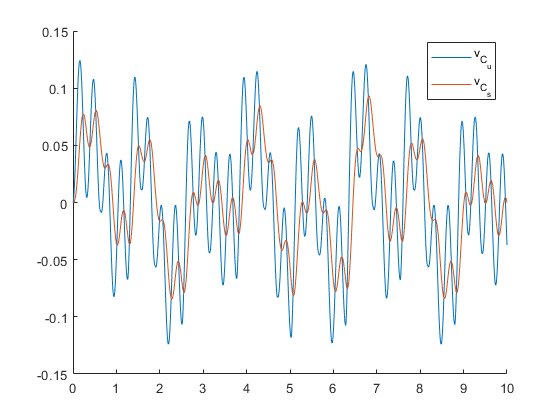
M_s = 300;
K_s = 2800;
B_s = 2000;
M_u = 30;
K_t = 21000;

global A B z_r;

A = [
    0,     -K_t,     0,      0
    1/M_u, -B_s/M_u, -1/M_u, B_s/M_u
    0,     K_s,      0,     -K_s
    0,     B_s/M_s,  1/M_s, -B_s/M_s
];

B = [K_t; 0; 0; 0];

z_r = @(t) (0.1 * sin(20 * t) + 0.03 * sign(sin(5 * t)) + 0.02 * sign(sin(2 * t)));

[t, x] = ode45(@suspension_system, [0, 10], [0; 0; 0; 0]);

figure;
fplot(z_r, [0, 10]);
legend("z_r");

figure;
hold on;
plot(t, x(:,1));
plot(t, x(:,3));
legend(["f_{L_t}", "f_{L_s}"]);

figure
hold on;
plot(t, x(:,2));
plot(t, x(:,4));
legend(["v_{C_u}", "v_{C_s}"]);

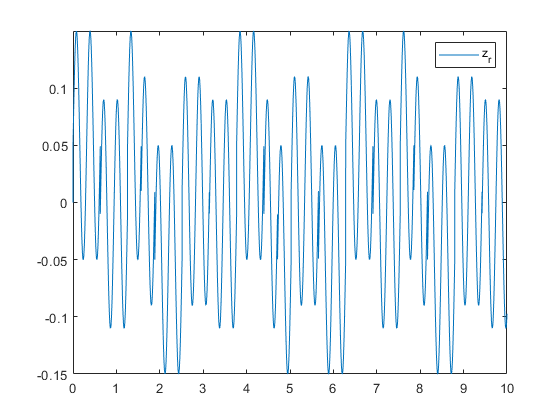
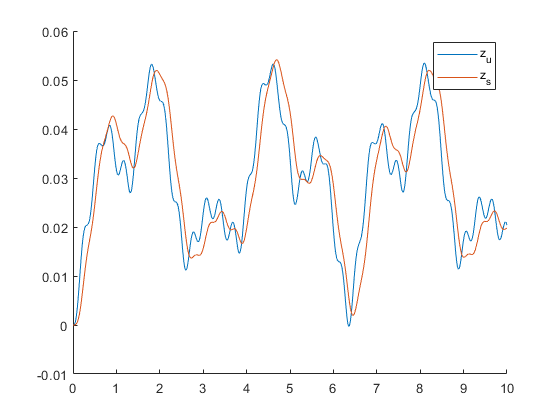
z_u = zeros([1, length(t)]);
z_s = zeros([1, length(t)]);
for i = 2:length(t)
    z_u(i) = trapz(t(1:i), x(1:i, 2));
    z_s(i) = trapz(t(1:i), x(1:i, 4));
end

figure;
fplot(z_r, [0, 10]);
legend("z_r");

figure;
hold on;
plot(t, z_u);
plot(t, z_s);
legend(["z_u", "z_s"]);

function dxdt = suspension_system(t, x)
    global A B z_r;
    dxdt = A * x + B * z_r(t);
end